KB ID 0000582
Problem
Given the amount of deployments I do, it’s surprising that I don’t use KMS more often. Like most technical types, I find a way that works for me, and that’s the way I do things from then on. However these last few weeks I’ve been putting in a new infrastructure for a local secondary school. Their internet access is through a proxy server, that refuses to let Windows activation work. Unfortunately the “Administrators” of this proxy server were not disposed to give me any help, or let me anywhere near it, to fix it.
So after activating a dozen servers over the phone, I decided enough was enough “I’m putting in a KMS Server!”
I’m deploying KMS on Windows Server 2008 R2, and it is for the licensing and activation of Serer 2008 R2 and Windows 7. I will also add in the licensing KMS mechanism for Office 2010 as well.
Note: If you are using Server 2003 it will need SP1 (at least) and this update.
Solution
To be honest it’s more difficult to find out how to deploy a KMS server, than it actually is to do. I’ve gone into a fair bit of detail below but most of you will simply need to follow steps 1-4 (immediately below). In addition, after that I’ve outlined how to deploy KMS from command line. Then how to test it, and finally how to add Microsoft Office 2010 Licenses to the KMS Server.
Install Microsoft Windows 2008 R2 Key Management Service (EASY)
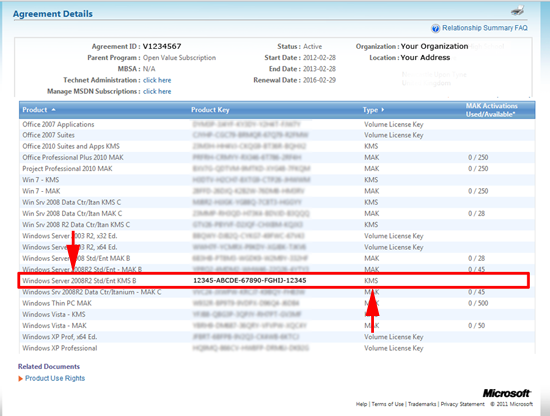
1. The most difficult part is locating your KMS Key! If you have a Microsoft License agreement, log into the the Microsoft Volume License Service Center, and retrieve the KMS License Key for “Windows Server 2008 Std/Ent KMS B”
Note: To License/Activate Server 2008 R2 AND Windows 7 THIS IS THE ONLY KEY YOU NEED. You do NOT need to add additional keys for Windows 7. (You DO for Office 2010, but I’ll cover that below).
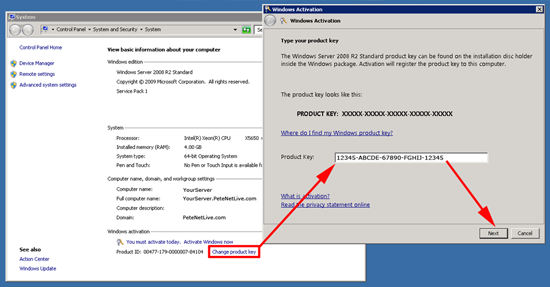
2. Armed with your new key, you simply need to change the product key on the server that will be the KMS server, to the new key. Start > Right Click “Computer” > Properties. (Or Control Panel > System). Select “Change Product Key” > Enter the new KMS Key > Next.
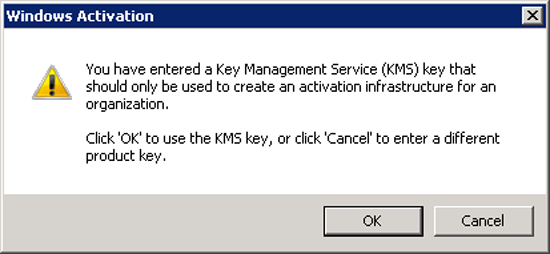
3. You will receive a warning that you are using a KMS Key > OK. You may now need to activate your copy of Windows with Microsoft, this is done as normal, if you can’t get it to work over the internet you can choose to do it over the phone.
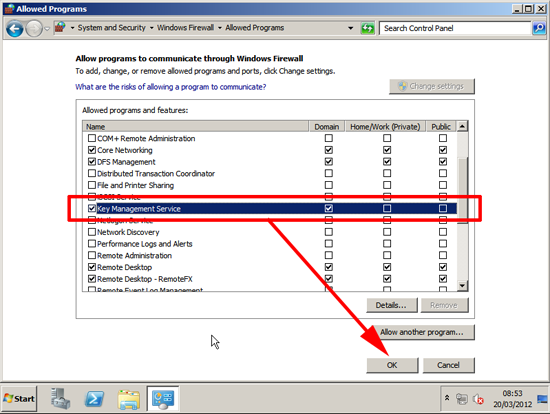
4. In a corporate environment (behind an edge firewall) you may have the local firewall disabled on the server. If you do NOT then you need to allow access through the local firewall for the “Key Management Service”, (this runs over TCP port 1688). To allow the service, Start > Firewall.cpl {enter} > Allow program or feature through Windows Firewall” > Tick Key Management Service > OK.
Note: Should you wish the change the port the service uses, you can do so with the following command, i.e. to change it to TCP Port 1024;
cscript c:\Windows\System32\slmgr.vbs /SPrt 1024
That’s It! That is all you should need to do, your KMS Server is up and running.
Install Microsoft Windows 2008 R2 Key Management Service from Command Line
You will notice below that I’m running these commands from command windows running as administrator (Right click “Command Prompt” > Run as administrator).
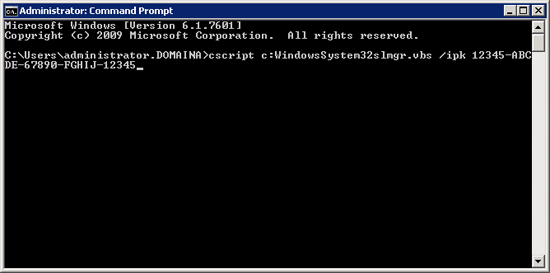
1. Locate your “Windows Server 2008 Std/Ent KMS B” Key > From command line issue the following command;
cscript c:\Windows\System32\slmgr.vbs /ipk XXXXX-XXXXX-XXXXX-XXXXX-XXXXX
Note: To License/Activate Server 2008 R2 AND Windows 7 THIS IS THE ONLY KEY YOU NEED. You do NOT need to add additional keys for Windows 7. (You DO for Office 2010, but I’ll cover that below).
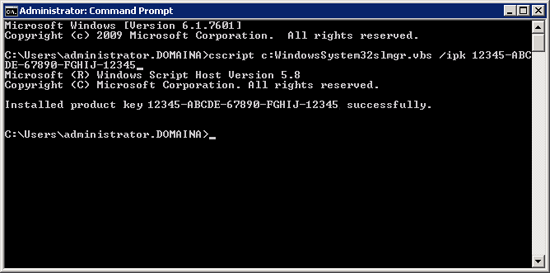
2. Providing the command runs without error, we have just changed the product key for this Windows server to be the KMS key.
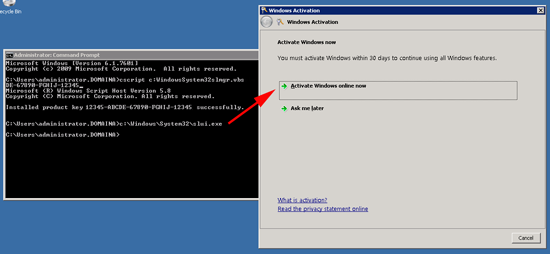
3. Now we need to activate the Windows Server > Run the following command;
c:\Windows\System32\slui.exe
Select “Activate Windows online now” > Follow the on screen prompts.
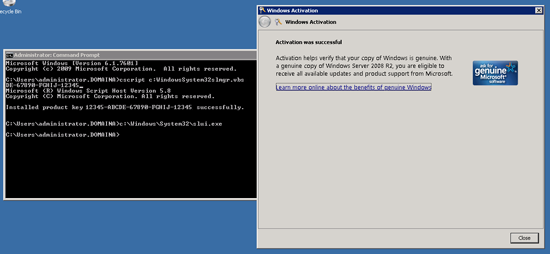
4. When complete, it should tell you that it was successfully activated.
5. In a corporate environment (behind an edge firewall) you may have the local firewall disabled on the server. If you do NOT then you need to allow access through the local firewall for the “Key Management Service”, (this runs over TCP port 1688). To allow the service, Start > Firewall.cpl {enter} > Allow program or feature through Windows Firewall” > Tick Key Management Service > OK.
Note: Should you wish the change the port the service uses, you can do so with the following command, i.e. to change it to TCP Port 1024;
cscript c:\Windows\System32\slmgr.vbs /SPrt 1024
That’s It! That is all you should need to do, your KMS Server is up and running.
Testing the Key Management Server
Before it will start doing what you want it to, you need to meet certain thresholds, with Windows 7 clients it WONT work till it has had 25 requests from client machines. If you are making the requests from Windows 2008 Servers then the count is 5. (Note: For Office 2010 the count is 5 NOT 25)
Interestingly: On my test network I activated five Windows 7 machines, then one server, and it started working.
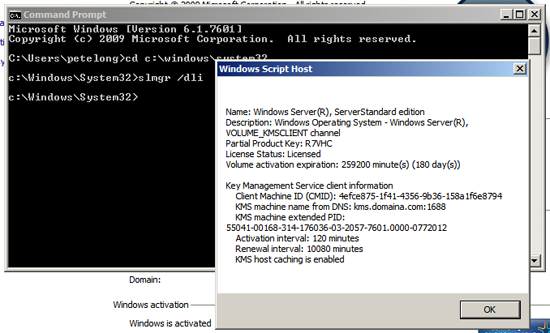
Windows 7 and Windows 2008 R2 have KMS Keys BUILT INTO THEM, if you are deploying/imaging machines you should not need to enter a key into them (unless you have entered a MAK key on these machines then you will need to change it to a client KMS Key). These are publicly available (see here).
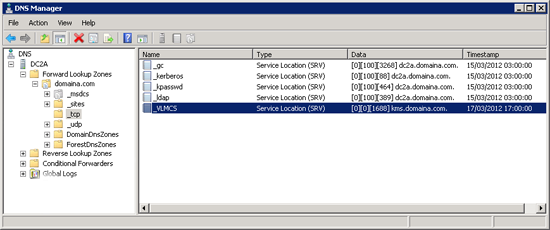
1. The service works because it puts an SRV record in your DNS, when clients want to activate, they simply look for this record before they try and activate with Microsoft, if they find the record, they activate from your KMS Server instead. If you look on your domain DNS servers, expand “Forward Lookup Zones” > {your domain name} > _tcp > You will see an entry for _VLMCS that points to your KMS Server.
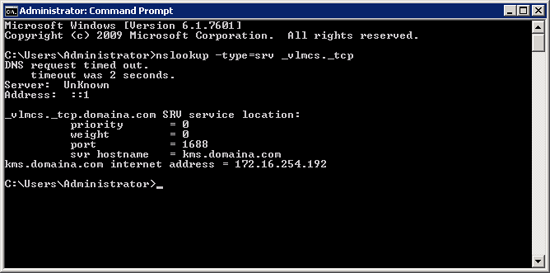
2. From your client machines you can test that they can see the SRV record, by running the following command;
nslookup -type=srv _vlmcs._tcp
Note: If this fails, can your client see the DNS server? And is it in the domain?
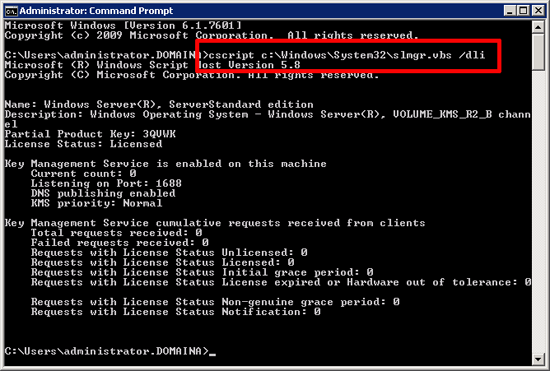
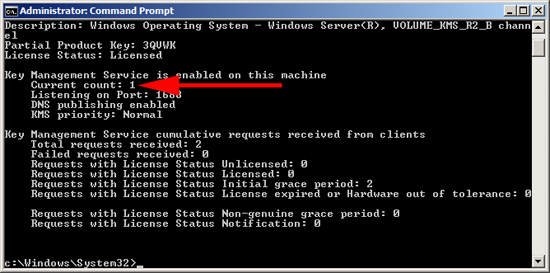
3. There is no GUI console for KMS to see its status, so run the following command on the KMS server;
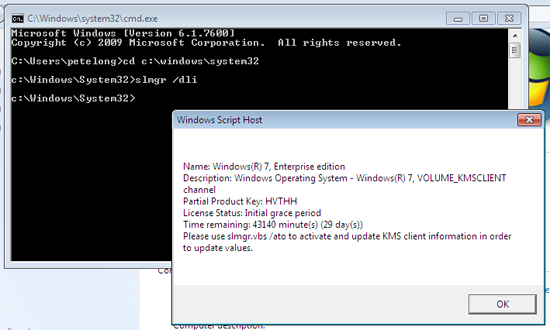
cscript c:\Windows\System32\slmgr.vbs /dli
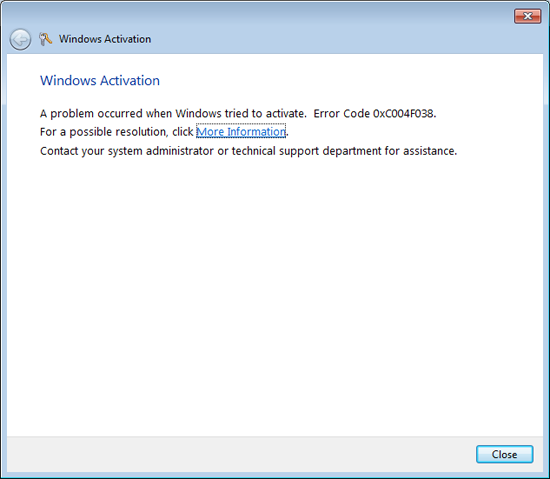
4. As I’ve mentioned above, with Windows clients you need 25, and Windows Servers you will need 5 requests before KMS will work, before this you will see;
Windows Activation
A problem occurred when Windows tried to activate. Error Code 0xC004F038
5. For each of these failures, look-in the KMS Server, and the “Current count” will increment by 1 till it starts to work). In a live environment this wont be a problem, (You probably wont be looking at KMS with less than 25 clients!). On a test network just clone/deploy a load of machines until you hit the threshold.
Troubleshooting KMS Clients
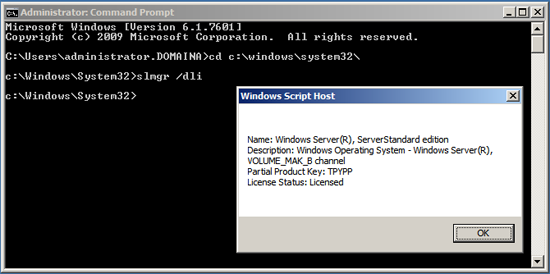
To make things simple the command to execute on the clients, is the same command that you run on the KMS server to check the status.
cd c:\windows\system32 slmgr /dli
For further troubleshooting, see the following links.
How to troubleshoot the Key Management Service (KMS)
Adding an Office 2010 KMS Key to Your KMS Server.
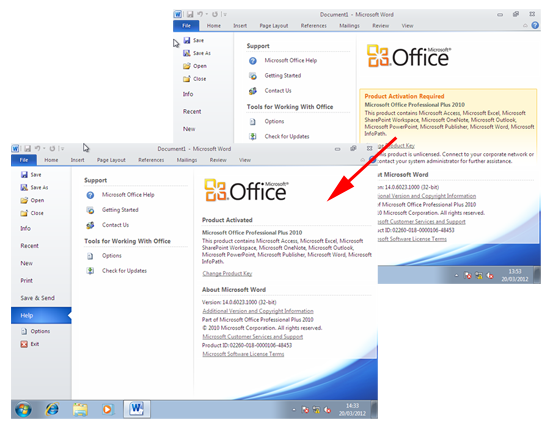
In addition to servers and clients, KMS can activate and handle Office 2010 licenses as well. You simply need to add in Office support, and your Office 2010 KMS key. As mentioned above, unlike Windows clients, you only need five requests to the KMS server before it will start activating Office 2010 normally.
If you want a KMS Server for JUST OFFICE 2010 and not Windows, then simply install and run the Office 2010 Key Management Service Host.
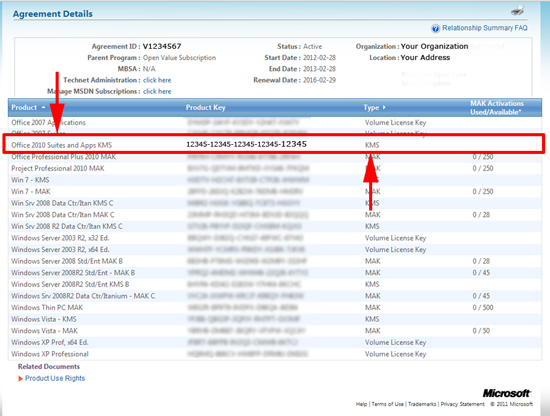
1. First locate your Office 2010 KMS Key! If you have a Microsoft License agreement, log into the the Microsoft Volume License Service Center, and retrieve the KMS License Key for “Office 2010 Suites and Apps KMS”
Note: As with Windows 7, and Server 2008 R2, Office 2010 comes with a KMS key already installed, if you have changed the key to a MAK key you can change it back using the Microsoft public KMS keys (see here).
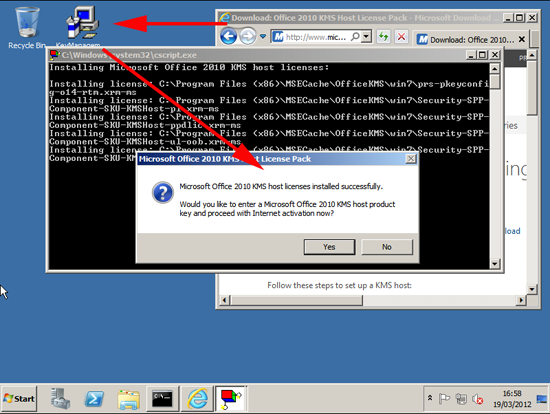
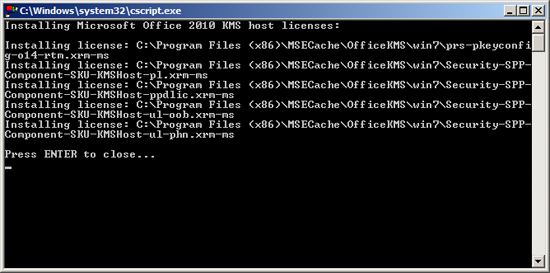
2. Download and run the “Microsoft Office 2010 KMS Host License Pack“.
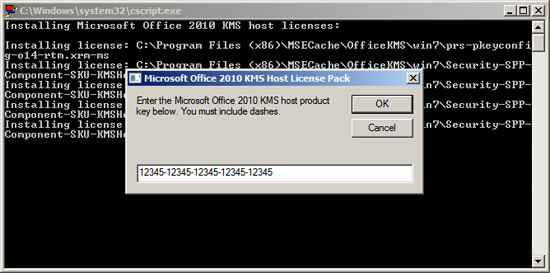
3. When prompted type/paste in your “Office 2010 Suites and Apps KMS” product key > OK.
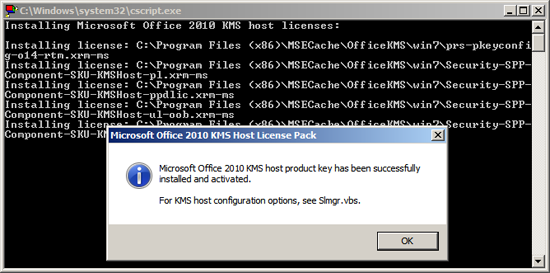
4. It should accept the key.
5. Press {Enter} to close.
6. Once you have five Office 2010 installations they should start to activate from your KMS server.
Troubleshooting Office 2010 KMS Activation
If you have a client that refuses to work you can manually force it to activate against your KMS server;
x64 Bit Clients. (Where kms.domaina.com is the FQDN of the KMS server)
cscript "C:\Program Files (x86)\Microsoft Office\Office14\OSPP.VBS" /sethst:kms.domaina.com cscript "C:\Program Files (x86)\Microsoft Office\Office14\OSPP.VBS" /act
x32 Bit Clients. (Where kms.domaina.com is the FQDN of the KMS server)
cscript "C:\Program Files\Microsoft Office\Office14\OSPP.VBS" /sethst:kms.domaina.com cscript "C:\Program Files\Microsoft Office\Office14\OSPP.VBS" /act
Related Articles, References, Credits, or External Links
KMS Activation – Error: 0xC004C008